21
2023
06

桥牌中总墩数定律的验证与解读

桥牌中总墩数定律的验证与解读

王玉富 陈鸿弋 王翰钊 蔡方平

桥牌中的总墩数定律是法国桥牌理论家让雷内·凡尔纳20世纪60年代发现的，20多年之后，被美国桥牌专家伯根及其搭档科恩发扬光大。
总墩数定律有多种不同的表述，其核心意思是：
任何一副牌，双方以各自配合最好的花色为将牌，双方期望得到的总赢墩数之和，与双方的将牌数之和大致相等。
为检验这个定律，我们得到北京新睿桥科技公司的大力支持，在他们提供的数万副随机牌例和双明手分析（DDS）数据的基础上，进行了数理统计计算。
1.构造随机变量与统计量
对任一副牌,设随机变量
X=南北方赢墩理论最大值+
东西方赢墩理论最大值
Y=南北方任一花色张数之和最大值+   
 东西方任一花色张数之和最大值
 Z=X-Y
对随机变量Z的一个容量为的n随机样本，构造统计量


随机选n副牌，根据DDS分析的数据，首先统计出随机变量Z样本值的分布表，进而计算出样本观察值均值和标准差这两个统计量。
2.万副牌样本统计结果

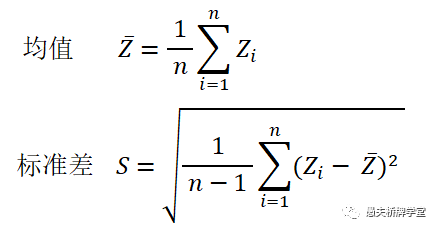
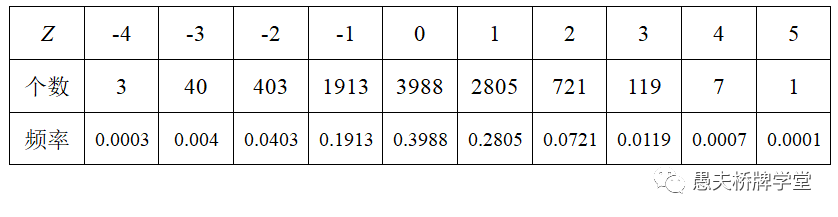
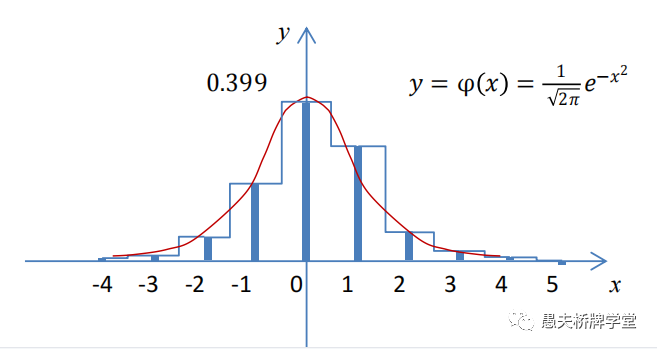
对一组10000副随机牌样本，通过对每一副牌用双明手分析软件分析并统计，得到如下分布表：

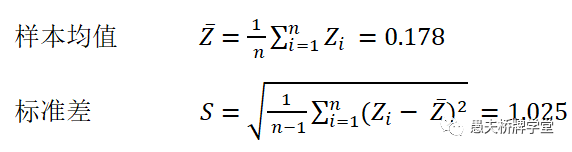
通过以上数据可以看出，这10000个样本中，有约40%的样本点正好符合定律（偏差为0）；偏差不超过±1墩的约占87%；偏差不超过±2墩的约占98.3%；偏差超过±2墩的样本占比不到2%；偏差超过±3墩的样本占比仅0.1%左右；没有出现偏差超过±5墩的样本点。
从统计数据及其直方图可以看出，随机变量Z非常接近于N(0,1)的正态分布。

3.典型牌例解读

下面我们首先来看这次统计的10000副牌中的前8副牌：

第1副：Z=(8+8)-(9+9)=-2

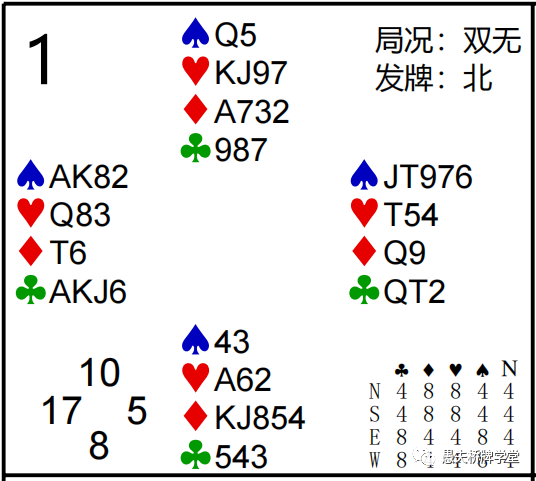
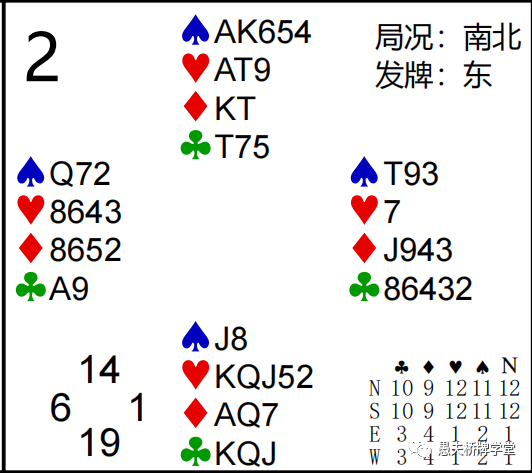
第2副：Z =(12+4)-(8+8)=0

第3副：Z =(7+11)-(8+9)=1  

第4副：Z =(7+10)-(8+9)=0

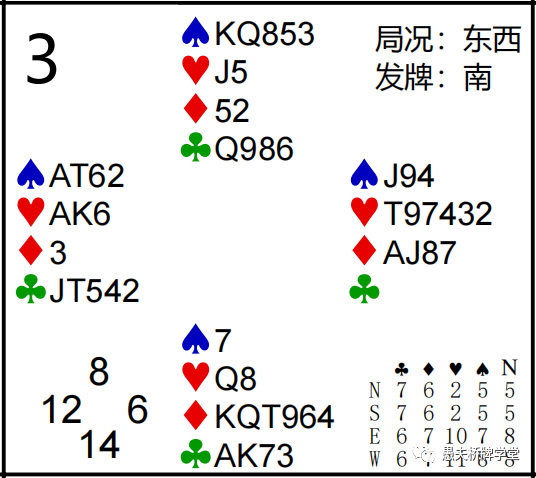
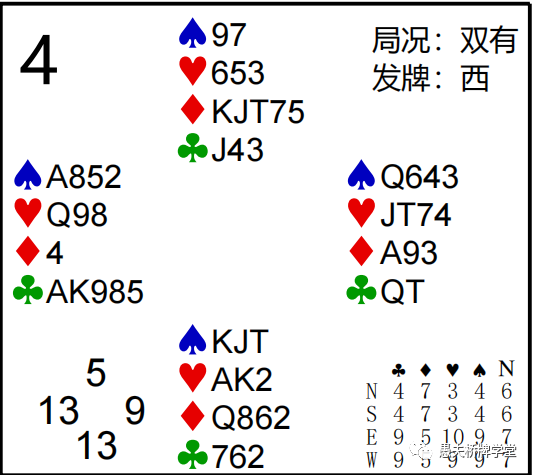
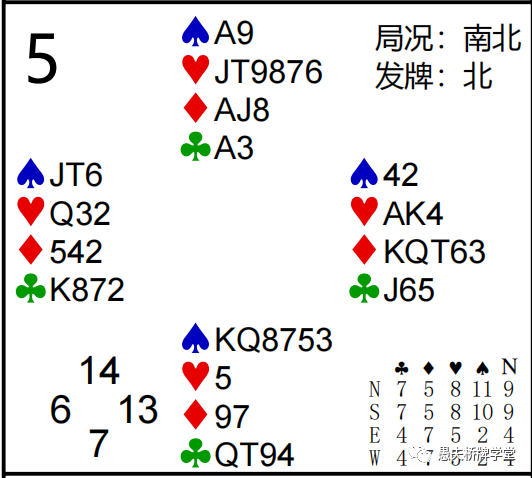
第5副：Z =(11+7)-(8+8)=2     

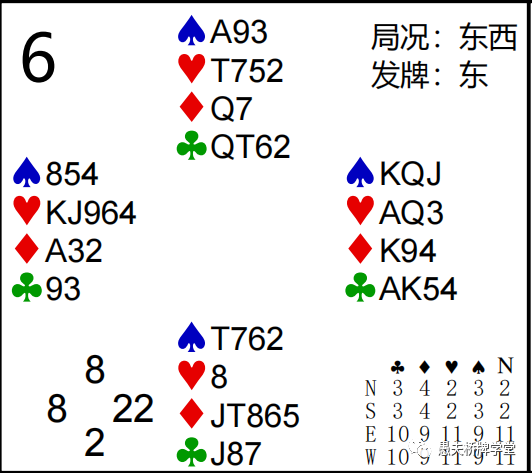
第6副：Z =(4+11)-(8+7)=0

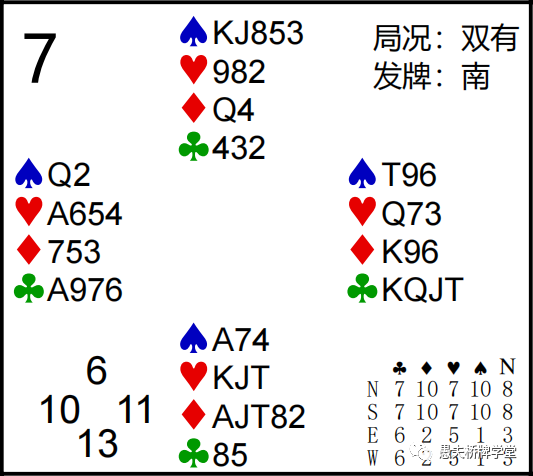
第7副：Z =(10+6)-(8+8)=0   

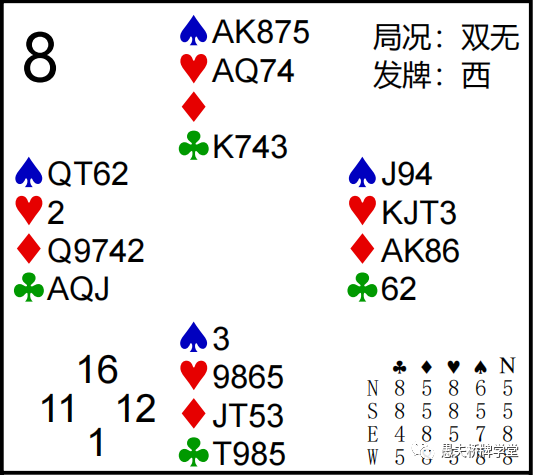
第8副：Z =(8+8)-(8+9)=-1

这8副牌都是比较常见的牌型，其中有4副牌的偏差为0；另外4副的偏差分别为±1和±2。
我们剖析一下第一副牌。
这一副北家的♠Qx双张对着南家的双张小牌，不仅这张Q的防守价值丧失，而且双张对双张还丧失了将吃的机会；东西方的♦花色也存在同样的情况。这副牌的理想“总墩数”比假定“将牌总数”之和少2墩（偏差为-2）。

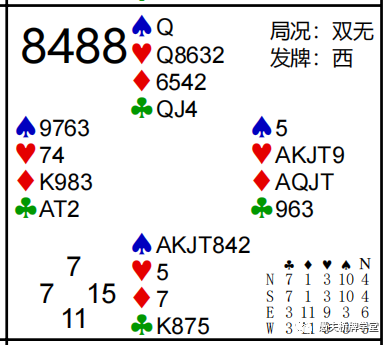
本次检验的10000个样本中，偏差最大的为+5(仅有1副)，是第8488副。

第8488副：Z=(10+11)-(8+8)=5  
这副牌南家的7411牌型并不是造成墩数偏差的主要因素，重要的是双方都有一门花色一手是单张，另一手是4张小牌（这门花色中没有一个大牌点）。这样在做庄时会产生大量的将吃赢墩。这种牌型对应斯普林特约定叫追求的低点力满贯的理想情况。
负偏差绝对值最大的为-4（共有3副），其中第1004副由于南家的♥KQ对着北家的单张小牌造成牌点的极大浪费，东西的♣单张对单张也丧失了将吃能力，这副牌造成理想的“总墩数”比“将牌总数”少了4墩（偏差为-4）。

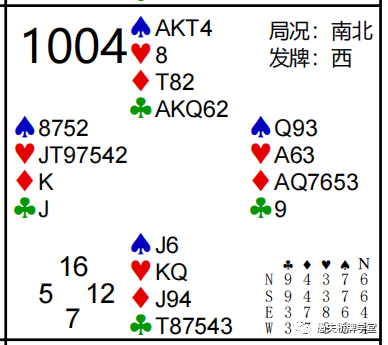
第1004副：Z=(9+8)-(11+10)=-4


必须强调指出的是，这种大偏差是极个别的现象，近90%的牌，偏差都在1墩以内；偏差超过2墩的比例不到2%；偏差超过3墩的基本上可以忽略。
另外，由于有些个别的牌例存在不同庄位赢墩数可能不同的情况，我们在构造随机变量Z时，又分别取不同庄位中理想赢墩数中的较小值或平均值，得到的分布表和直方图的对称性更好，与标准N（0,1）正态分布贴合得更好，甚至某些大样本（20000个）中，竟然没有出现一个偏差达到5的样本点。



我们用多组数据进行了反复检验，没有发现有明显差异的情况。
因此，从统计学的角度，我们完全可以认为总墩数定律是可信的，其所有的偏差，都属于“微小的偶然误差”。
牌手竞叫时，应该在总墩数定律原则的指导下，根据自己的持牌和叫牌中获得的其他三人牌型方面的信息，及时对心目中的“总墩数”进行调整。
4.用总墩数定律指导竞叫

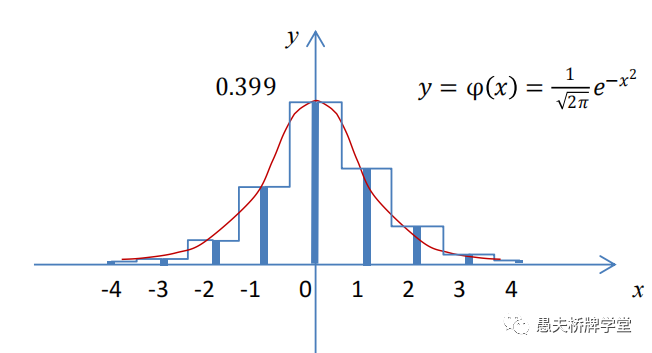
一般来说，每一副牌每一方的两家，至少有一门花色达到7张配合，通常有8张、9张甚至10张以上的配合。总墩数定律结合二三法则，可以确定我们一方应该竞叫到的大致阶数。

(1)双方大牌点基本相等（18,19,20,21点的情况）：总墩数定律支持双方各自叫到自己与同伴最长一门花色张数之和的阶数。一般来说，有7张将牌配合，可能完成一阶花色定约；8张配合可能完成二阶花色定约；9张配合可能完成三阶花色定约；10张配合，则可能完成四阶高花成局定约。这是现代叫牌法中针对5张高花体系的伯根加叫的依据。

通常情况下，双方都有8张或更多的花色配合，总墩数大于16，双方都可以完成二阶花色定约。但若没有更多的将牌配合，完成三阶定约就有困难。这也是常说的“平牌争二不争三”的道理。

(2)双方牌点相差一张K或A的实力（一方23-24点，另一方16-17点）。

①如果双方都是普通8张配合，总墩数仍为16。牌点较高的一方有望赢得9-10墩；牌点较低的一方大概只能赢得6-7墩。牌点高的一方进局有风险，如果叫到四阶高花，牌点低的一方通常不应该做“牺牲叫”，除非自己一方有10张以上配合。

②如果双方都是9张或10张配合，总墩数达到18-20,牌点高的一方可以轻松完成四阶高花定约，牌点低的一方可以根据局况做出合理的牺牲。

(3)一方牌点达到成局标准（一方25点以上一方15点以下），这时牌点高的一方成局是必然的。即使没有8张以上花色配合，通常也能完成3NT定约。牌点低的一方，如果有牌型优势，例如有9张以上配合有单缺，就应该尽量提前做出破坏性的“牺牲叫”，这是现代叫牌理论中跳加叫作为牺牲叫的理论依据。

(4)在竞叫过程中，要根据叫牌获得的信息和自己的牌型，对“总墩数”和本方的“赢墩数”进行调整。主要有以下几个方面要考虑。

①对方的长套花色中，有单张K、Q或双张KQ、QJ、Qx等不利因素，本方期望的赢墩数下调1墩。

②将牌数达到9时，若有一家是3张以上小牌，另一家是单张，本方赢墩数上调1墩；另一手是缺门时，本方赢墩数上调2墩。

③单张对单张小牌、双张对双张小牌时，赢墩数下调一墩；另一手有K、Q时，下调2墩。两手牌型完全相同下调2墩。


本篇文章来源于微信公众号:                 愚夫桥牌学堂

作者:wzmcc | 分类:叫牌 | 浏览:11620 | 评论:0
« 上一篇 下一篇 »

发表评论:

◎欢迎参与讨论，请在这里发表您的看法、交流您的观点。

您是本站第1601名访客 今日有0篇新文章